Imagem: Mars 2020 Perseverance Launch Panorama, United Launch Alliance.

No dia 30 de Julho de 2020 a NASA lançou uma nova missão a Marte, Perseverance. O objetivo dessa viagem é estudar a geologia e o clima do planeta vermelho, bem como procurar por sinais de vida. O tema "viagens espaciais" sempre gera uma grande curiosidade, afinal de contas não é todo dia que a gente assiste essas missões ambiciosas.

Muitas pessoas, inclusive, principalmente aquelas que cresceram nos anos 80 e 90, acreditando nas promessas dos filmes e programas de TV, podem se perguntar: se a tecnologia está disponível há tanto tempo, por que a exploração espacial não é mais comum?

É evidente que existem complicações logísiticas e monetarias para excursões desse tamanho, mas muito se engana quem pensa que lançamentos espaciais são raros, só em 2023 o mundo lançou quase 3 mil objetos ao espaço:

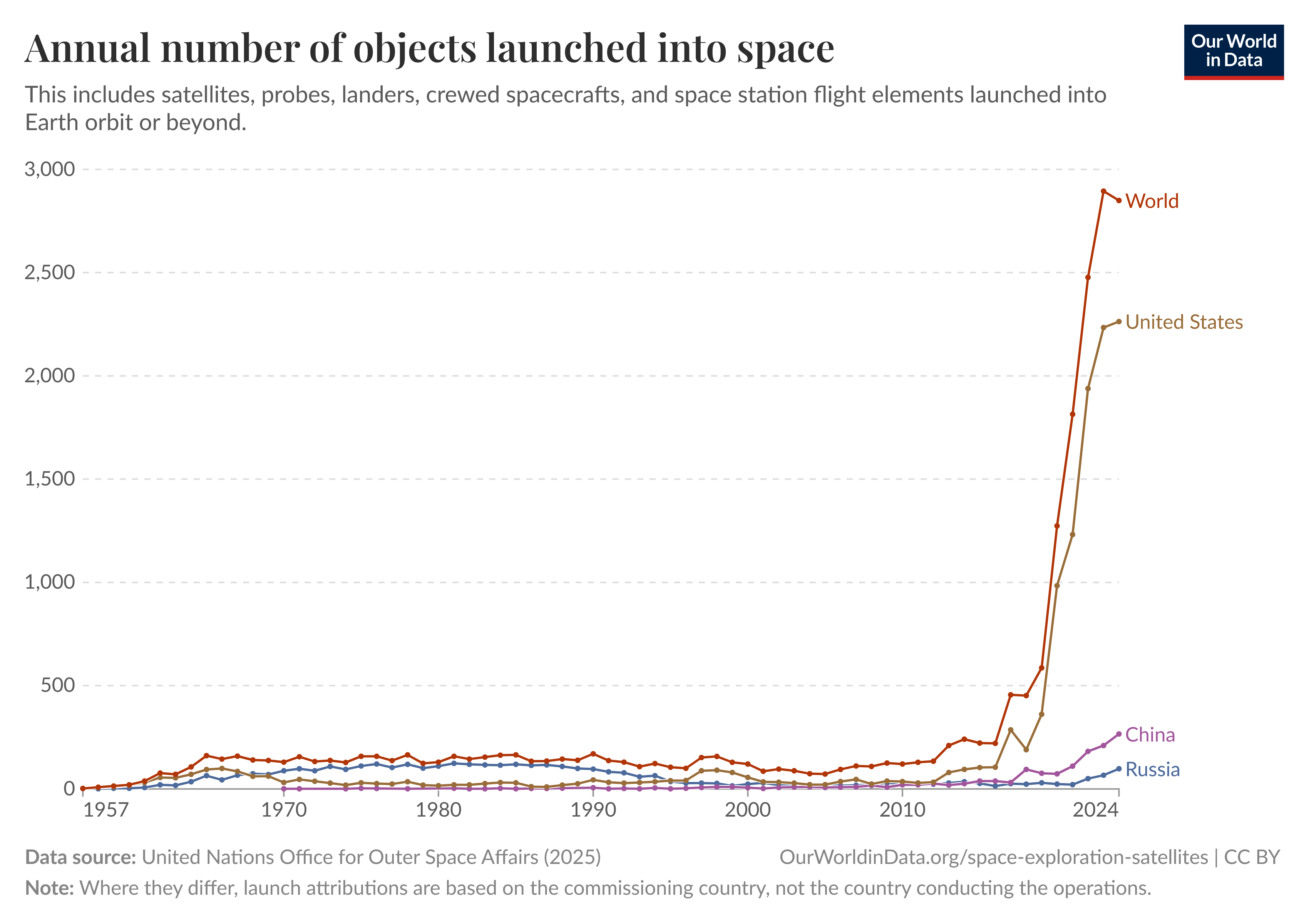
Quantidade de lançamentos espaciais por ano, por país, desde 1957.
Fonte: Our World in Data.

Isso acontece porque uma série de indústrias, em especial de telecomunicações, dependem de lançamentos que, embora bem menos heróicos do que está no imaginário popular, aproveitam de todo aquele conhecimento da corrida espacial e além. Vamos falar, portanto, sobre o que é necessário para sair da órbita terrestre. Mas, antes, falemos de como surgiu essa história toda...

A corrida espacial da guerra fria

O que conhecemos como Guerra Fria, foi o período entre o fim da Segunda Guerra Mundial (1939 – 1945) até quase o final do século XX, em que as duas principais potências mundiais da época, os Estados Unidos, representando o bloco capitalista, e a URSS, representando o bloco socialista, disputaram a hegemônia global. "Fria" remonta ao fato de que não houve um conflito militar direto entre as duas potências.

Pode se dizer que o principal motivo disso é o fato de que ambos polos eram – e ainda são – grandes potências nucleares, de forma que um confronto direto significaria uma escalada nuclear e, possivelmente, o fim do mundo como o conheciamos. A disputa tomou, portanto, rumos mais criativos, como o desenvolvimento tecnologico e a corrida espacial.

Embora o uso de foguetes tenha começado com o lançamento de fogos de artifício em datas comemorativas, as aplicações militares não demoraram a aparecer, fruto, principalmente, de esforços alemães durante a 2a GM. Os cientistas nazistas, inclusive, foram amplamente disputados por ambos os lados, dada a sua expertise com lançamentos, e participaram ativamente da corrida espacial, que começou oficialmente com o lançamento do Sputnik 1, em 4 de Outubro de 1957, pela União Soviética: o primeiro objeto feito pelo homem a orbitar a Terra. Na sequência os Estados Unidos criaram a NASA para disputar essa fronteira tecnológica, com isso dando início a conquistas alternadas, como enviar os primeiros animais ao espaço, depois os primeiros humanos e ainda o primeiro pouso na lua e em outros planetas. A corrida espacial se tornou um fim em si próprio, a ponto de que quando a situação geopolítica se apaziguou, os blocos começaram a cooperar mais no espaço.

Imagem conceito do projeto Apollo-Soyuz, um aporte entre a estação americana com a estação soviética.
Fonte: NASA Imagem de Davis Meltzer

Com o fim do conflito, toda tecnologia e conhecimento produzidos por um período de grande investimento em ciência e engenharia estava disponível para gerar riqueza para os Estados Unidos, o vencedor da Guerra Fria. Isso abriu a porta da exploração comercial do espaço por inúmeras aplicações, como o GPS e a TV.

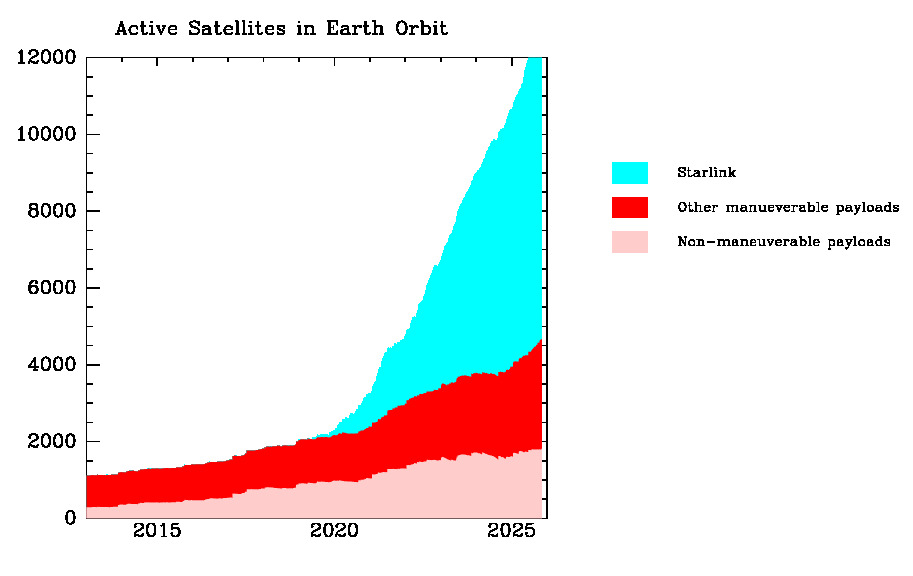
Número de satelites na órbita da Terra.
Fonte: Jonathan McDowell

Hoje, lançar um satelite pro espaço é uma operação ordinária, principalmente depois que a Starlink começou a operar (que foi, ironicamente, um pouco depois que eu escrevi esse texto originalmente) e a SpaceX ajudou a baratear o custo do lançamento com "foguetes reutilizáveis". Esses fatos não são necessariamentes positivos, mas essa discussão está fora do escopo do texto.

Um outro aspecto em que a pesquisa espacial influencia nossa vida é na criação de inúmeras tecnologias e patentes, afinal, não basta simplesmente mandar uma pessoa pra ISS, você precisa garantir que ela sobreviva, também. Infelizmente, essa última parte é um privilégio humano, visto que o primeiro ser vivo a ir pro espaço, a cachorrinha Laika, morreu no processo, conforme o planejado.

"Laika, a primeira viajante do cosmos".
Fonte: Wikipedia/Colectivul Dumitrana

Nesse processo de garantir a sobrevivência dos astronautas, nós precisamos reinventar coisas triviais, por exemplo, existe uma anedota muito famosa (e muito falsa) sobre como a NASA gastou milhões para desenvolver uma caneta que funcionasse no espaço, enquanto que os cosmonautas simplesmente usavam lápis. Algumas dessas adaptações e tecnologias criadas para acomodar os pesquisadores que se aventuram no espaço acabam, de fato, ficando disponíveis para o público amplo - elas recebem o nome de "spinoffs”.

Inclusive, se você está pensando no astronauta brasileiro, Marcos Pontes, e seu “Travesseiro da NASA”, tenho boas notícias pra você: a “Espuma com memória” dos travesseiros foi, realmente, desenvolvida pela NASA (agência espacial), e não pela NASA (Nobre e Autentico Suporte Anatômico), para aumentar o conforto e segurança nos veículos aéreos.

As vezes é difícil de acreditar que esse cara foi nosso ministro.
Fonte: AMT Online

A Física de um lançamento

Já deu pra entender um pouco da história dos lançamentos espaciais, agora vamos ao que interessa:

Como lançar um foguete?

Tudo começa, como muita coisa na física, com Isaac Newton e suas três leis do movimento: a Lei da Inércia, que diz que um corpo em descanso permanecerá em descanso, até que uma força seja aplicada nele, e um corpo em movimento permanecerá em movimento, até que uma força seja aplicada nele. A Lei da Ação e Reação, que diz que toda ação gera uma reação igual em modulo e oposta em sentido. Mas a mais famosa é, sem dúvidas, a Segunda Lei, aquela equação que diz que a força resultante em um objeto é igual à sua massa vezes a sua aceleração:

Por mais notória que seja essa definição, ela não corresponde ao que Newton postulava. A formulação original fala, na verdade, que essa força é a variação do momentum, também conhecido como quantidade de movimento:

Matematicamente, uma variação é modelada através de uma ferramenta chamada "derivada", que é essa "fração" na fórmula (espero que nenhum professor de cálculo me veja falando que é uma fração). Na prática, estamos perguntando quanto uma grandeza muda num dado intervalo de tempo:

A grande "sacada" da derivada é dizer que esse intervalo de tempo é muuuuuito pequeno, o que nos permite uma série de recursos algébricos. Um deles é descobrir a variação de uma grandeza composta por duas outras grandezas que variam no tempo, justamente o caso da quantidade de movimento, que é definida pela massa vezes a velocidade:

Para resolver esse problema, o cálculo nos manda fazer a seguinte conta:

Aplicando para $q$:

Na maioria dos problemas de física do ensino médio a massa é constante, o que zera o primeiro termo da equação; como a variação da velocidade é a aceleração, chegamos ao resultado mais conhecido de "$F = ma $". Mas o nosso objeto de estudo hoje não segue esse paradigma: uma grande parte da massa de um foguete é seu combustível, que é queimado de forma muito acelerada, fazendo com que a variação da massa não seja desprezível.

Para entender melhor todo o processo, vamos construir um modelinho bem simplificado das fases de um lançamento espacial e quais forças agem sob o foguete durante esse período.

Antes de decolar

Para simplificar um pouco as coisas, vamos imaginar que o foguete está em pé no chão, como em um desenho animado. Nesse caso existe uma única força principal atuante: o peso do foguete, que puxa o foguete em direção à Terra.

Surge, ainda, pela terceira lei, uma força de reação, chamada de força normal, que empurra o foguete contra o chão. A forma como eu gosto de pensar nessa força é o chão resistindo contra a compressão do foguete, ou seja, evitando de ser esmagado pelo peso daquele objeto.

Voltando à segunda lei, devemos equacionar o somatório de forças à variação na quantidade de movimento, mas o foguete está parado. Pensando no sentido comum do termo "quantidade de movimento": um foguete parado não tem nenhuma quantidade de movimento - ele nem sai do lugar - e, portanto, a sua variação, é, também, nula:

O Peso, P, está aplicado no centro de gravidade do foguete e seu valor é dado pela massa do foguete, vezes a capacidade de atração que a Terra é capaz de exercer naquele ponto da sua superfície. À esta capacidade damos o nome de gravidade:

Ligando os sistemas de propulsão

Motores ligados, tudo ok, é hora de partir!

Da mesma forma que um carro, o movimento do foguete também é fruto da combustão. Diferente de um carro, porém, a explosão não movimenta pistões: a explosão em si (e com quanto vigor ela consegue "expulsar" os gases de exaustão) que gera o movimento.

Outra diferença é que aqui na Terra os carros têm amplo acesso ao oxigênio que permite a combustão, o mesmo não vale para foguetes no vácuo, que precisam levar seu próprio oxigênio, além do combustível.

A combustão, representada pela equação química genérica e não balanceada acima, é uma reação exotérmica em que um hidrocarboneto reage com oxigênio, formando água e gás carbônico. Os foguetes podem ter combustível líquido ou combustível sólido.

Os foguetes de combustíveis líquidos costumam ser mais pesados e complexos, afinal, são precisos dois tanques, um para o comburante, que normalmente é o Oxigênio, e outro para o combustível, que costuma ser Querosene. A vantagem é que, como combustível e comburente estão separados, é possível ter um maior controle da reação, ajustando as proporções da mistura e, se necessário, até interrompendo a reação.

Os foguetes de combustível sólido são bem mais simples, visto que o "sólido" ao qual nos referimos é um cilindro feito da mistura combustível-comburente. Embora mais leves, esse tipo de veículo fornece muito menos controle sobre a reação - uma vez que ela começa, é muito difícil de pará-la.

Como mencionei, os gases de exaustão oriundos da combustão literalmente empurram o foguete para cima, seguindo a terceira lei de Newton: conforme os gases são expelidos para fora, eles geram uma força contrária tentando levantar o foguete. Nesse primeiro momento, porém, sem tirar o veículo do equilíbrio (ou seja, sem alterar a quantidade de movimento):

Como podemos ver na equação, o peso, a força de reação do fluído, $F_{fluido}$, e a normal formam uma conta de soma zero. Como o peso é mais ou menos fixo (fora a pequena variação de massa do combustível, mas, nesse primeiríssimo momento, essa é pequena), a "briga" fica entre a força do fluído e a força normal: tanto maior é a tentativa de se sair do chão, menor é a compressão feita sob ele (e, portanto, sua reação). Isso acontece até que a força do fluído seja igual ao peso do foguete e a normal se anula.

A força que esse fluído exerce é uma soma de dois termos, o da saída de gás de exaustão, calculado pelo produto entre a taxa de variação da massa do fluído em relação ao tempo, $ \dot{m} $, e a velocidade de saída do fluído, $v_f$, e o do efeito da diferença de pressão, que é o produto entre a área do bocal de saída do fluído, $ A_e $, e a diferença de pressão do bocal, $\Delta P $:

O bocal ao qual eu me refiro é o canal que faz o escape dos produtos da combustão. Note que esse canal, que nada mais é que um tubo, tem um formato bastante específico à fim de alavancar fenômenos geométricos de fluídos - como como eles se comportam ao atravessar por diâmetros menores ou maiores, modelado pelo Princípio de Bernoulli - de forma que ele começa na câmara de combustão, passa por uma garganta (diâmetro reduzido), cuja função é acelerar o gás, e em seguida termina com uma abertura divergente (diâmetro aumentado), que expande o gás.

Esse tipo de bocal, chamado de Bocal CD (Convergente-Divergente), comprime o gás para deixá-lo mais rápido e em seguida expande ele para reduzir sua temperatura e pressão. Embora essa segunda parte possa parecer contraintuitiva olhando para a equação, visto que mais pressão significa mais força, a redução é importante para reduzir o impacto nos materiais do foguete: o fluído supera a velocidade do som, o que gera ondas de choque e aquecimento aerodinâmico que podem causar danos estruturais.

Voar, voar, subir, subir...

Eventualmente o sistema de propulsão atinge seu objetivo e faz o foguete alçar voo: isso acontece quando a força do fluído, que passarei a chamar de Força de Impulso, $F_{I}$, supera o peso do sistema, tirando o sistema de equilíbrio.

Voltando àquela definição meio coloquial que a gente estava usando, o foguete começa a se movimentar (a variação da quantidade de movimento deixa de ser nula):

$$\sum F = F_I - P = \dot{m} v + ma$$

Forças, velocidades, acelerações e até mesmo áreas são vetores, isso significa que eles não são simplesmente números. Eles são números com propósito - eles têm um sentido e direção. Não basta dizer que estou andando a 10 kilometros por hora, também preciso dizer para onde.

Normalmente representamos vetores por setas, tanto nas ilustrações do foguete que eu fiz, quanto na notação matemática: $\vec{F}$, $\vec{v}$ e $\vec{a}$. Vamos reescrever nossa resultante com vetores:

$$\sum \vec{F} = \vec{F_I} - \vec{P} = \dot{m} \vec{v} + m\vec{a}$$

A importância dos vetores é que a segunda lei de Newton é verdadeira para cada eixo de um sistema de coordenadas: você faz o somatório das forças na vertical, para descobrir quanto o foguete sobe ou desce, e o somatório na horizontal para descobrir quanto ele anda para a direita ou para a esquerda. Eu estava omitindo essa representação porque nós estávamos apenas em um único eixo, o vertical, então não precisávamos nos preocupar, mas, conforme o foguete ganha velocidade, Forças Aerodinâmicas começam a aparecer também na horizontal.

Forças Aerodinâmicas são aquelas que surgem da interação do foguete com a atmosfera: a Força de Arrasto, que é o atrito da fuselagem do veículo conforme ele atravessa o ar, e a Força de Sustentação, que é um efeito de "levantamento" causado pelo formato das asas - é exatamente a força que permite que o avião voe.

O arrasto, assim como o atrito, é uma somatória de pequenas forças que agem da interação entre o fluído (o ar) e um objeto atravessando ele (o foguete). Como dois corpos não podem ocupar o mesmo espaço, para chegar a uma nova posição, é preciso deslocar o ar que antes estava ali.

Medições sobre o efeito da resistência do ar em veículos costumam ser feitas com modelos em túneis de vento.
Fonte: NASA Imagem de Eric James

Sabe quando você está tentando andar contra o vento? Aquela dificuldade que você está sentido é exatamente o arrasto. Foguetes são corpos carenados (é o que popularmente chamamos de um objeto aerodinâmico), isso signfica que seu formato reduz o arrasto, mas, ainda assim ele está presente. A fórmula do arrasto é dada por:

$$\vec{F_a} = -\frac{1}{2} C_a A_a \rho \vec{v}^2$$

Note que o arrasto depende estritamente da velocidade, $v$, que está ao quadrado - ela é o termo mais importante da equação e quem dita a direção da força: à rigor, o arrasto é uma força contrária ao movimento (por isso o sinal de menos). Temos ainda o Coeficiente de Arrasto, $C_a$, que é uma medida do "quão aerodinâmico é aquele corpo", normalmente medido em túnel de vento, e a Área de Arrasto, $A_a$, que é a área que está em contato com o ar, gerando aquele atrito.

O último termo desconhecido, que merece seu próprio parágrafo, é a densidade do fluído, $\rho$. Junto da gravidade (aliás, justamente por conta dela), é isso que diferencia lançar um foguete na Terra ou em Jupiter, ou então o início do lançamento e o final. Quanto mais densa for a atmosfera, maior é a sua resistência ao movimento do foguete. Conforme nos afastamos da superfície da Terra, o efeito da gravidade é menor e os gases que compõem a atmosfera ficam mais dispersos - ou seja, a densidade do ar é maior na superfície do que na estratosfera, até chegarmos ao espaço, onde não há atmosfera e nem arrasto.

Quando uma asa corta o ar, sua geometria faz com que o ar que passa por cima da asa e o ar que passa por baixo tenham velocidades diferentes; consequentemente, a pressão local também é diferente. Essa diferença de pressão gera a Força de Sustentação, que vai da pressão menor para a maior:

$$\vec{F_s} = \frac{1}{2} C_s A_s \rho \vec{v}^2$$

Na fórmula, $A_s$ representa a área da asa e $C_s$ é o coeficiente de sustentação, normalmente medido experimentalmente.

Isso significa que enquanto um aerofólio precisa ser projetado para manter uma alta pressão em cima da asa, de forma que a força resultante vai jogar o carro para baixo, a geometria de uma asa deve fazer o inverso, deixando a pressão alta para baixo, o que faz com que a força resultante seja para cima e permita o vôo de um avião, por exemplo.

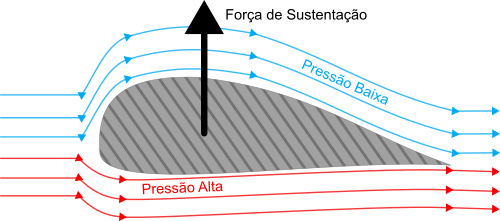
Nos foguetes, a força resultante é lateral fazendo efeito no controle e estabilidade do veículo, ao invés de auxiliar na subida. Além das asas, a direção e estabilidade são feitas por Motores Vernier, que são motores menores capazes de alterar a trajetória do vôo, ou, mais recentemente, por bocais com juntas rotacionais, que permitem direcionar o fluxo de gás que impulsiona o foguete pra cima. Para simplificar um pouco as contas, vamos considerar que um desses mecanismos estejam sendo aplicados, de forma a cancelar perfeitamente a força lateral de sustento:

$$\vec{F_{vernier}} = - \vec{F_s}$$ Agora, podemos juntar tudo!

Como nós consideramos um sistema de controle utópico, capaz de manter o foguete completamente estável, só precisamos nos preocupar com uma direção, a vertical. Nesse caso, nossa resultante toma a seguinte forma:

$$\sum \vec{F} = \vec{F_I} - \vec{P} - \vec{F_a} = \frac{dq}{dt}$$

Substituindo as fórmulas já descritas:

$$\dot{m}_{fluido} \vec{v_f} + \Delta P A_e - m\vec{g} - \frac{1}{2} C_a A_a \rho \vec{v}^2 = \dot{m} \vec{v} + m \vec{a}$$

A partir daí precisamos fazer algumas considerações:

1. No nosso modelo a taxa com que o foguete perde massa é a taxa com que fluído da combustão é expelido, ou seja: $\dot{m}_{fluido}=\dot{m}$. Isso nem sempre é verdade, podemos lembrar, por exemplo, dos foguetes com multiplos estágios, que vão deixando partes pelo caminho.
2. Não podemos dizer que a gravidade e a densidade do ar são constantes, porque nós estamos nos afastando da Terra, então ambas são, também, função do tempo: $g(t)$ e $\rho (t)$.
3. Talvez seja contraintuitivo, mas a velocidade do foguete não é a mesma velocidade de saída do fluído. Basta lembrar que no início da decolagem, quando o foguete ainda está bem devagar, o fluído já está sendo expelido com bastante vigor.
4. A aceleração é a variação da velocidade, $\vec{a} = \frac{d\vec{v}}{dt}$.

Levando estes pontos em consideração:

$$\dot{m(t)} \vec{v_f}(t) + \Delta P A_e - m(t)\vec{g}(t) - \frac{1}{2} C_a A_a \rho(t) \vec{v(t)}^2 = \dot{m(t)} \vec{v(t)} + m(t) \frac{d\vec{v}}{dt}$$

Essa expressão gigante é uma Equação Diferencial Ordinária - a ferramenta que usamos para descrever o mundo!

As EDOs são equações que envolvem funções e suas derivadas, é o caso tanto da velocidade, $v$, que se apresenta em três termos, ao quadrado, ela própria e sua derivada; quanto da massa, $m$, que também apresenta sua derivada primeira, $\dot{m}$. Essas equações são notoriamente difíceis de resolver e, embora existam muitos métodos para soluciná-las de forma exata (leia-se algebricamente), em grande parte dos casos reais precisamos partir para soluções numéricas, o que significa usar o computador para chegar a resultados aproximados. Vamos falar mais dessas ferramentas em posts futuros, mas, por hora, basta dizer que resolver essa equação é tão complicado quanto parece.

Ao infinito e além!

Eventualmente, chegamos ao espaço, para fora da influência da gravidade da Terra e no vácuo, de forma que os termos com $\rho$ e $g$ na equação do vôo acima zeram, ou, de forma mais específica, o foguete para de ser influenciado pela força peso e pelo arrasto:

$$\sum \vec{F} = \vec{F_I} = \frac{d\vec{q}}{dt}$$

Olha, que ótima notícia: toda força de impulso é transformada em quantidade de movimento - e bem a tempo, porque o combustível já estava acabando. Pela primeira lei de Newton sabemos inclusive que a quantidade de movimento se mantém, então, podemos, inclusive, parar os foguetes e apenas aproveitar da velocidade que já desenvolvemos na subida:

$$\sum \vec{F} = \frac{d\vec{q}}{dt} = 0$$

Note que a variação da quantidade de movimento é zero, não a quantidade de movimento em si: essa é o valor da massa do foguete vezes a velocidade do foguete no momento em que desligamos os motores - e assim será até que liguemos eles novamente, ou alguma outra força externa seja aplicada no veículo.

Conclusões

Espero que tenha ficado claro que mandar um foguete é, ao mesmo tempo, trivial e complexo. Trivial porque acontece quase todos os dias, nós realmente aperfeicoamos a arte de mandas coisas para o espaço, o que não significa que o processo seja simples. Esse post tentou mostrar apenas uma pequena parte da dificuldade em fazer esses lançamentos: as equações que o descrevem, mas existe ainda toda a engenharia de materiais, desenvolvimento de sistemas de controle, gerenciamentos das cadeias logísticas para cada peça e equipamento e muitos outros fatores.

Isso tudo só para falar da ida. Uma missão como a Perseverance, tem cada pequeno detalhe planejado, desde onde o robô deveria aterrisar em Marte, até quais ferramentas ele teria ao seu dispor, como ele enviaria resultados de testes para a Terra e o que ele faria se perdesse conexão conosco.

Uma selfie do robô Perseverance e do drone Ingenuity.
Fonte: NASA/JPL-Caltech/MSSS

Não era minha premissa criar um guia completo, até porque não sou qualificado para isso, mas espero ter fornecido um pouco mais de contexto sobre o que acontece, dum ponto de vista físico, em um lançamento espacial.

Para aqueles que desejem estudar um pouco mais, o recurso que baseou o texto inteiro foi o Guia de Foguetes para iniciantes da NASA, eu recomendo a leitura do material.